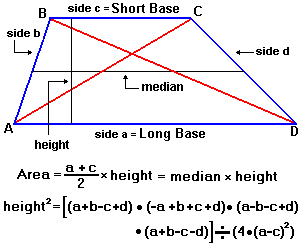
\(S= \frac {1}{2} (a+c) \times h=l \times h\)
\(h^2=[(a+b-c+d) \cdot (-a+b+c+d) \cdot (a-b-c+d) \cdot (a+b-c-d)] / (4 \cdot (a-c)^2)\)
使用这个计算器需要知道梯形的4个边
线 BC 和 AD 是平行的,称为底边
线 AB 和 DC 称为梯形的腰
线 AC 和 DB 称为对角线
垂直于 AD 、 BC 的线叫梯形的高
平行于AD 、 BC,位于 AB 和 DC 中间的线叫做梯形的中位线
中位线\(l = \frac {AD + BC}{2}\)
输入数据:
长度=8
边b=4
短底=4
边d=3
点击“计算”,输出数据
周长=19
中位线=6
高=2.7811
面积=16.686
角A=44.049
角B=135.95
角C=112.02
角D=67.976
对角线AC=5.831
对角线BD=7.4162
与小伙伴分享:
◎已有0人留言