黎曼函数（Riemann function）是一个特殊函数，由德国数学家黎曼发现提出，黎曼函数定义在[0,1]上，其基本定义是：R(x)=1/q，当x=p/q(p,q都属于正整数，p/q为既约真分数)；R(x)=0，当x=0，1和(0,1)内的无理数。黎曼Zata函数（s）的定义如下：设一复数s其实数部分＞1而且：
定义在区间[0,1]上的函数R(x)：
当x=p/q(p,q都属于正整数，p/q为既约真分数)时，R(x)=1/q；
当x=0,1和无理数时，R(x)=0称为黎曼函数
从黎曼函数的定义可知，它具有如下一些特征：
（1）黎曼函数是区间[0,1]上的有界函数，其上确界是1/2，下确界是 0 ，其值域只有一个，聚点是0，它也是数列{1/q}的极限值，其中q为自然数。
（2）黎曼函数在有理点的图象关于直线x0=1/2对称。
（3）对于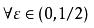 
，使得R(x)=R（p/q）=1/q>ε）的区间(0,1)中的有理数只有有限多个。
黎曼zeta函数参数 =55
点击"计算"，输出结果
逼近的Zeta函数 (55) = 1, n=20000
与小伙伴分享：
◎已有0人留言